単利と複利はどう違う？

金利の付き方には2つのタイプがあります。「単利」と「複利」です。資産運用の知識がある方は、「複利の効果」という話を聞いたことがあるかもしれません。資産運用では、「金利の付き方」を理解しておく必要があります。

金利は一般的に年利率で示される

「金利」とは、預金や債券の利子や、借入金に対する利息です。元本に対する金利の割合は、利率（利子率）ですが、これを金利と呼ぶ場合もあります。

利率は、「％」で表されます。特に断りがなければ、1年あたりの利率、つまり「年利率」で示されます。年利率のことを「年利」と呼びます。年利１%というのは、元本が例えば100万円なら、「１年あたり1万円の利子がつく」という意味です。

ただし、年利は、預入期間に注意しなければなりません。

仮に、年利１％の６ヵ月定期預金を例に考えてみましょう。１年間預けたら１％の金利がつきますが、預入期間が半年なので、利子も年1万円の半分です（本来、利率は日割りで計算しますが、ここでは単純化して1年の半分として説明します）。

計算式は、「100万円×1％÷2＝5千円（税引前）」となります。

単利と複利の違い

では、年利１％で100万円を3年間預けた場合、受け取れる利子はいくらでしょうか。

簡単でしょ、今度は3倍すればいいんでしょ。「100万円×1％×3＝3万円（税引前）」と言いたいところですが、冒頭で、利子の付き方には2つのタイプがあるとお伝えしましたね。

それが、「単利」と「複利」です。

「単利」は、投資した最初の元本に対して、利子を計算する方法です。年利1％であれば、元本100万円に対して、1年間に1万円（税引前、以下同様）。2年目の1年間にも1万円、3年目にも1万円。そうです。先ほど計算したのは「単利」で、「100万円×1％×3＝3万円」です。

一方、「複利」は、ついた利子をその都度元本に加え、次の計算期間には加算された利子と元本に対して利子を計算する方式です。利子の計算期間によって、1ヵ月複利、半年複利、年複利などがあります。ここでは、年複利で計算例を見ていきましょう。

【年複利による毎年の利子額】

1年目：1,000,000円×1%＝10,000円（→2年目の元本の一部になる）

2年目：1,010,000円×1%＝10,100円（→3年目の元本の一部になる）

3年目：1,020,100円×1%＝10,201円

【3年分の利子】

10,000円＋10,100円＋10,201＝30,301円

先に計算した「単利」に比べて、利子は301円多くなっています。

3年とは言わず、これを長期間繰り返すと、複利の利子は雪だるま式に増え、単利との差はどんどん開いていきます。また、例では年利1%の年複利で計算しましたが、年利率が高ければ高いほど、複利効果は大きくなります（グラフ）。

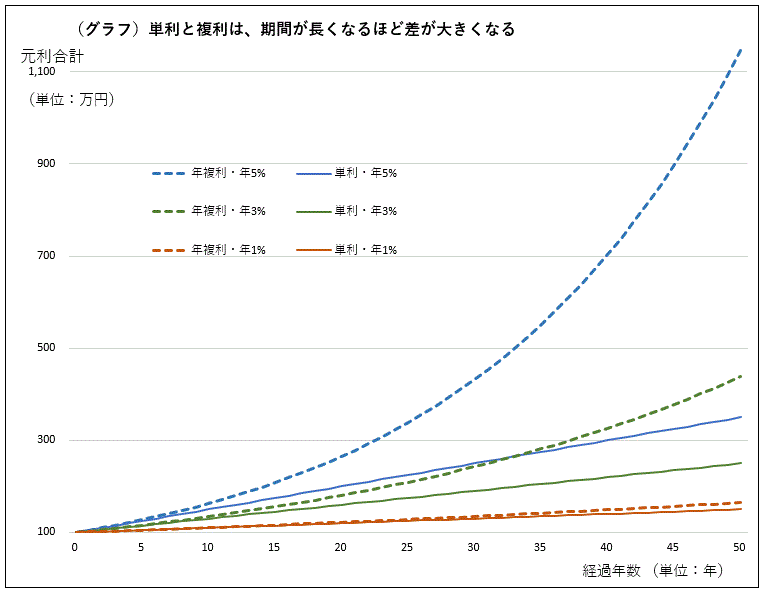
なお、ここでは計算しやすいように、年複利を例に挙げました。一般的に銀行の定期預金は、半年複利です。半年後に、年利の半分の利子がつき、その利子が元本に加算されて新たな元本額となり、次の半年分の利子を計算します。年複利に比べて利子が加わるペースが速いので、雪だるまも早くふくれ上がります。

その昔、証券会社に「中期国債ファンド」という、多くの投資家が利用していた公社債投信がありました。当時は高金利だっただけでなく、この金融商品は1ヵ月複利でした。日々の運用から生まれた収益分配金を月末にまとめて、翌月の元本に加算するのです。引き出しやすい上に、雪だるまがどんどん膨れるため、多くの人が利用していた人気商品でした。

現在でも、証券総合口座の中で資金をプールする「MRF（マネー・リザーブ・ファンド）」が、毎日決算をして発生した収益分配金を月末にまとめて再投資しています。しかし分配率が低いので、今のところ目立った1ヵ月複利の効果は期待できません。

まとめ

金利は、特に断りがなければ、年利率で示されます。表示された利率がそのまま受け取れるのではなく、日割りで預入期間に応じて利子の金額が計算されます。利子のつき方には、「単利」と「複利」の2種類があります。複利は、利子がつく都度、次の計算期間の元本に加えられるため、利子が雪だるま式に膨れあがります。複利では、利率が高いほど、また、投資期間が長いほど、高い効果が得られます。